Задача комівояжера: Ідея розв’язання задачі з одним кубітом

Опубліковано: at 08:00

tps-one-qubit

Задача комівояжера (TSP) є класичним NP-складним завданням у комбінаторній оптимізації. Формулюється вона так: маємо набір «міст», які необхідно відвідати, при цьому кожне місто повинно бути відвідано рівно один раз, і в кінці подорожі комівояжер повертається до стартової точки. Завдання — відшукати найкоротший (або найдешевший) маршрут, що задовольняє цим умовам.

Оскільки для TSP не існує відомого поліноміального алгоритму в класичному обчислювальному середовищі, дослідники шукають шляхи прискорення на квантових комп’ютерах. Утім, багато сучасних квантових реалізацій TSP ґрунтуються або на використанні великої кількості кубітів (Ising-моделі, QUBO-постановки), або на багатокубітних схемах (gate-based), що стає критичним обмеженням для реальних експериментів.

Ідея розв’язання задачі з одним кубітом

Автори пропонують свіжий підхід, у якому всі міста кодуються станами одного кубіта на сфері Блоха. Ключові моменти:

  1. Стан кубіта як «місто»

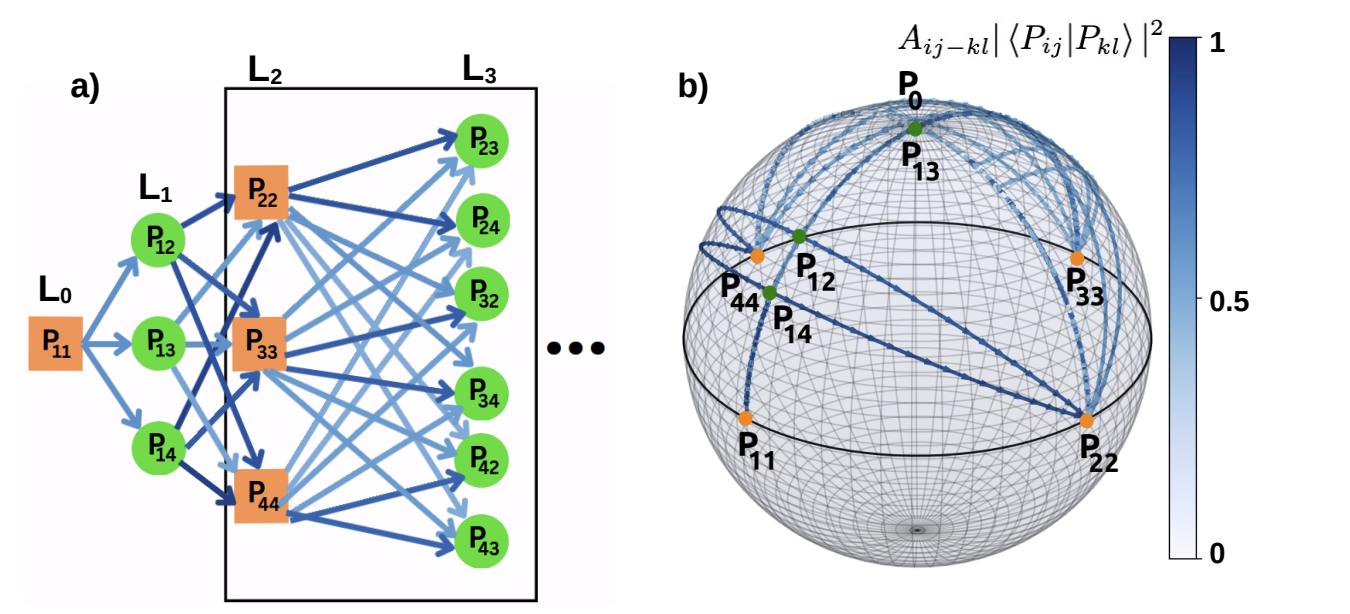
    • У статті показано, що можна відобразити кожне місто (точку на площині для класичної постановки) на певний стан кубіта (точку на сфері Блоха).
    • При цьому відстані між містами відображаються на «геодезичні» відстані між станами кубіта.

  2. Перехід між містами

    • Автори застосовують серію квантових операторів обертання (rotation operators) U, щоб «переводити» кубіт зі стану, що відповідає одному місту, у стан, який відповідає іншому.
    • Якщо розглядати класичні алгоритми, то вони перевіряють усі можливі маршрути послідовно (або за певною стратегією). Натомість у квантовому підході завдяки принципу суперпозиції кубіт може одночасно охоплювати декілька можливих під-маршрутів.

  3. Суперпозиція усіх можливих шляхів

    • На відміну від «перебору» кожного шляху окремо, одиночний кубіт готується у такому стані, що містить «комбінації» всіх можливих маршрутів. У класичній аналогії це було б схоже на те, щоб «пройти всі маршрути одночасно».
    • У підсумку, змінюючи (оптимізуючи) параметри обертання, дослідники отримують стан із переважаючою ймовірністю відповідати саме найкоротшому маршруту.

  4. Оптимізація та оцінка результату

    • Щоб знайти оптимальні параметри, автори застосовують метод SPSA (Simultaneous Perturbation Stochastic Approximation) – це різновид стохастичного алгоритму оптимізації, який добре працює з шумними або високовимірними просторами параметрів.
    • Після серії обертань виконується вимірювання (наприклад, повна томографія стану кубіта). Зі стану кубіта «зчитують», які міста мають найбільшу амплітуду ймовірності формувати валідний маршрут, — і це дає змогу відновити шуканий цикл комівояжера.

Основні результати

  1. Економія ресурсів. Натомість інших квантових підходів, що вимагають багатьох логічних (і фізичних) кубітів, у цій роботі запропоновано використання одного кубіта. Це радикально скорочує потреби у ресурсах, оскільки керувати та коригувати один кубіт легше, ніж велику кількість.
  2. Висока точність для невеликих прикладів. У межах випробувань було успішно розв’язано приклади TSP до 9 міст із точністю 90+% (у більшості випадків алгоритм точно знаходить оптимальний маршрут). Автори наголошують, що це краще за низку існуючих квантових методів на сьогодні.
  3. Потенціал масштабування. Хоча квантова схема з одним кубітом видається простою, дослідники припускають, що її можна доповнити багатокубітними взаємодіями або орієнтувати на масштабніші оптимізаційні задачі. При цьому вже базова однокубітна структура може дати поліноміальне прискорення у порівнянні з чисто класичними алгоритмами.

Чому це важливо?

Виклики та перспективи

  1. Проблеми шуму: хоча однокубітна система значно зменшує негативний вплив декогеренції, безідеальність обертань та неточні вимірювання все одно можуть призвести до помилок у визначенні оптимального маршруту.
  2. Складність масштабування: збільшення кількості міст у TSP експоненційно збільшує кількість можливих маршрутів. Попри заявлену імовірну поліномійну перевагу, для великих TSP потрібно ретельніше вивчати стабільність алгоритму, зміну параметрів оптимізації та «застрягання» у локальних мінімумах.
  3. Розширення на інші задачі: метод поки що зосереджений на TSP, але його можна адаптувати під інші NP-складні завдання чи задачу пошуку (графи, розфарбовування графів, тощо). Автори припускають, що таку суперпозиційну ідею можна масштабувати із залученням декількох кубітів і контролюваних двокубітних операцій.

Висновки

Запропонований авторами підхід є яскравим прикладом, як, використовуючи виключно принцип суперпозиції, можна скоротити обчислювальні витрати при розв’язанні задачі комівояжера. Однокубітне кодування маршрутів на сфері Блоха обіцяє зменшення ресурсів, відносно високу точність і потенційний програш у часі (порівняно з класичними алгоритмами) при пошуку оптимального маршруту серед експоненційної кількості варіантів.

Якщо цей метод буде реалізовано на квантових процесорах із кращими показниками когерентності й мінімізованими шумами обертання, він може стати конкурентним інструментом комбінаторної оптимізації вже в найближчі роки. Водночас потрібні подальші дослідження для перевірки придатності цього методу на практиці й для узагальнення на ширший клас складних задач.

Ключовий висновок: навіть один кубіт, якщо використовувати його «правильно» (через глибоку суперпозицію станів і спеціальні оптимізаційні процедури), може відкривати нові можливості в розв’язанні задач, що традиційно вважаються складними або неможливими для класичних алгоритмів у поліноміальний час. Це ще раз підкреслює, що квантові обчислення — це не лише багатокубітні процесори, а й пошук нових творчих рішень в існуючих апаратних рамках.

Посилання на оригінальну роботу:
Goswami K., Veereshi G. A., Schmelcher P., Mukherjee R. “Solving The Travelling Salesman Problem Using A Single Qubit,” arXiv:2407.17207 (2024).